上 三角形 合同 条件 407443-三角形 合同条件 三辺相等
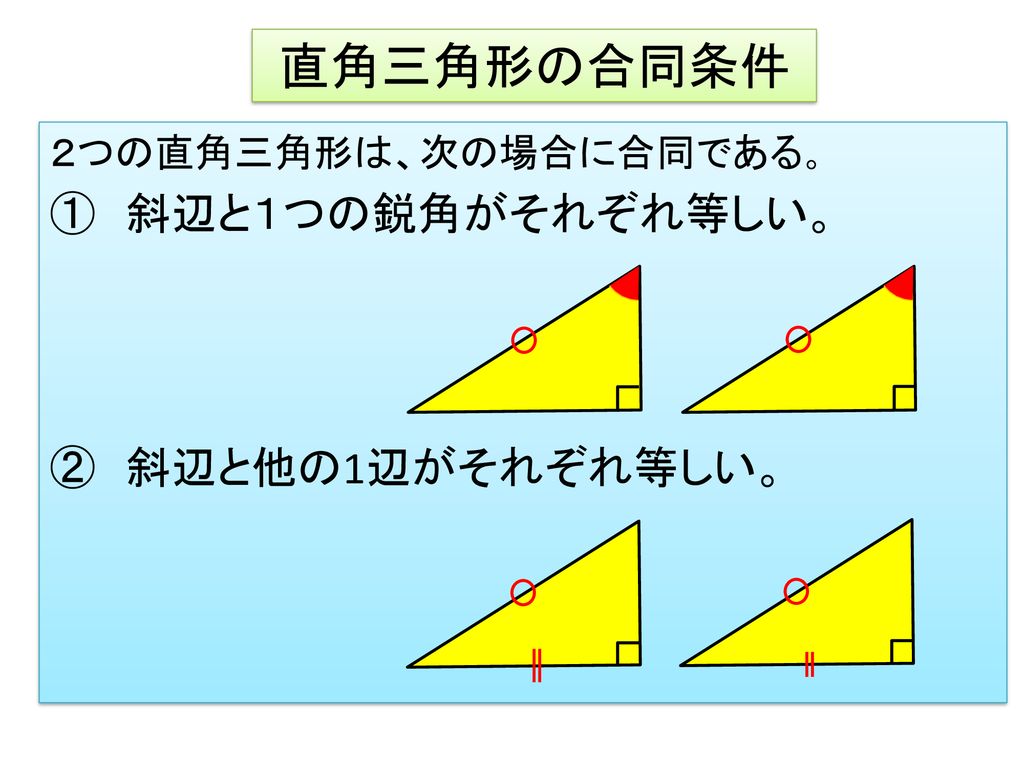
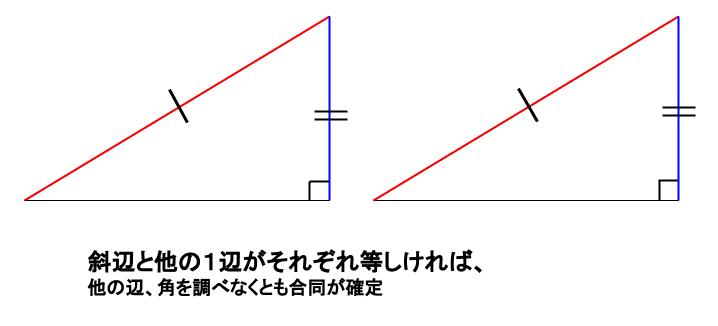
ユウマ君とアキラ君が1~6の条件にしたがって三角形をかきます。 2人がかいた三角形は、必ず合同になるか、ならないかを答えなさい。 合同になる場合は、その合同条件も答えなさい。 1 角度がそれぞれ、30°,50°,100°の三角形 直角三角形の合同条件には次の \(2\) つがあります。 条件①斜辺と 1 つの鋭角がそれぞれ等しい \(1\) つの角が直角(\(90^\circ\))であることから、斜辺の長さおよび \(1\) つの鋭角が等しいことが示せれば、 残りの \(1\) 角も自ずと定まります 。 そのため、一般的な合同条件③「\(\bf{1}\) 三角形の成立条件に登場する不等式を三角不等式といいます。三角不等式は様々な「長さ」に拡張されています。 →いろいろな三角不等式(絶対値,複素数,ベクトル) 三本の不等式を a a a について解くことで,条件を ∣ b − c ∣ < a < b c bc

中学校数学 証明のコツ 直角三角形の合同条件 と その利用の仕方 を自学自習できる教材
三角形 合同条件 三辺相等
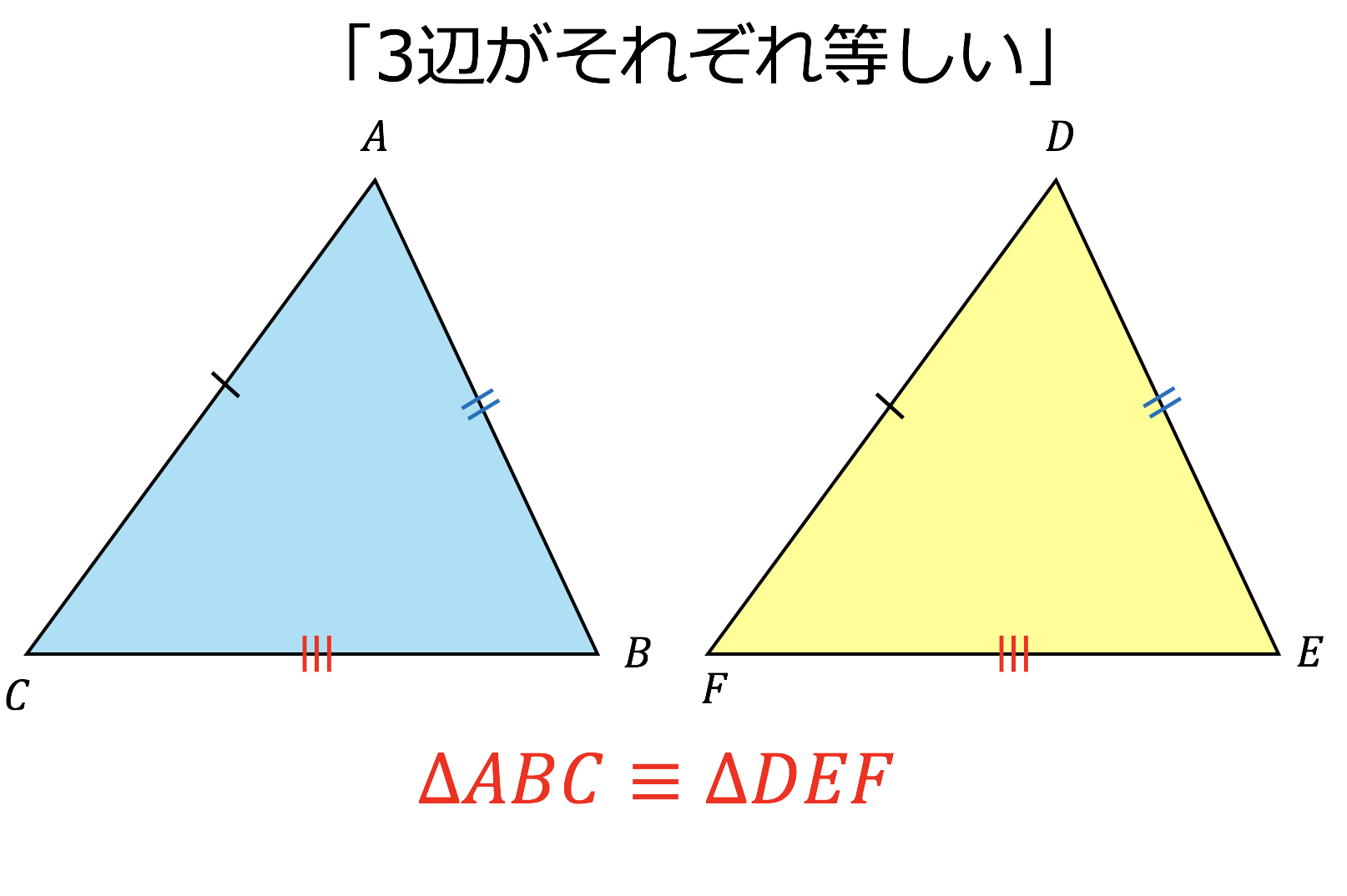
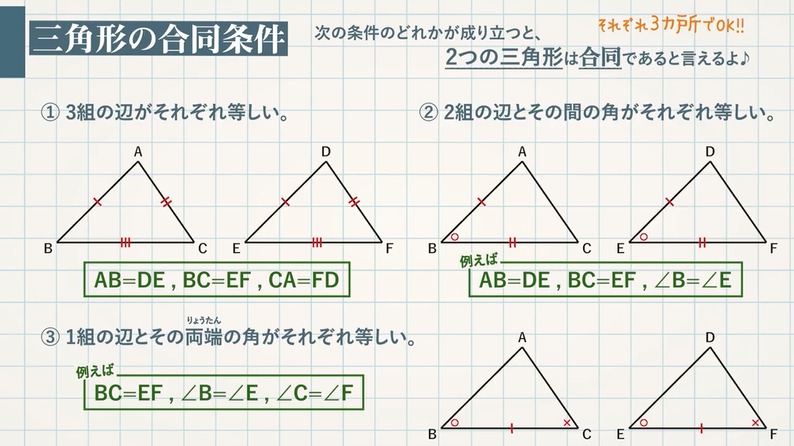
三角形 合同条件 三辺相等-円と三角形 > 円にかかわる三角形の合同を証明してみましょう。 2つの図形ががぴったりと重なることを合同(ごうどう)といい、記号で「≡」と表します。合同のとき、対応する辺や角が等しくなります。三角形の合同条件 次のどれかが成り立つと2 三角形の「合同条件」と「相似条件」 を勉強してきたよね。 両方とも数学の証明のために必要なアイテムだから、テスト前には覚えなきゃいけないね。 念のためおさらいしておくと、 三角形の合同条件 3つの辺の長さがそれぞれ等しい;




直角三角形の合同条件 証明のときに直角三角形が出てきたらこれ 中学や高校の数学の計算問題
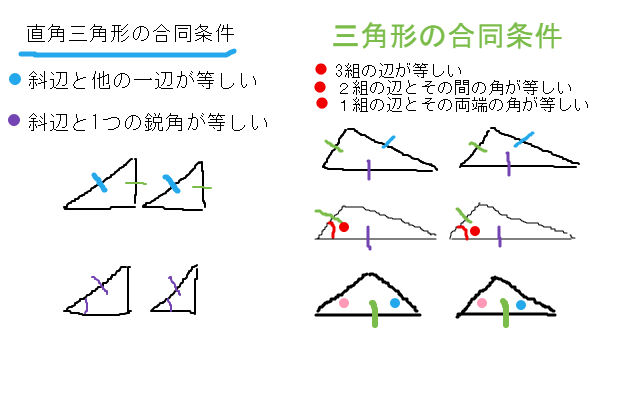
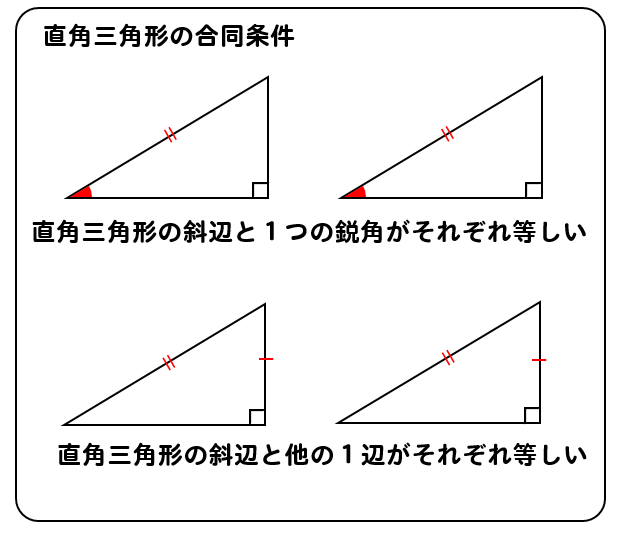
三角形の合同条件 チェックボックスで合同条件を1つ選びます。次に点a, b, cを動かすと合同条件に応じて点a', b', c'も変わります。現れたa', b', c'や辺、角の大きさを見て、 a'b'c'を abcと合同にできそうか考えてみましょう。なお点a', b', c'を動かして、点の位置や辺の向きなどを変えることもでき三角形 四角形 三角形の内角の和 𝟖 ° 平行四辺形 定義2組の対辺がそれぞれ平行な四角形 三角形の外角は、それととなり合わない 2つの内角の和に等しい 2組の 対辺はそれぞれ等しい 三角形の合同条件① 3組の辺がそれぞれ等しい 今回は中2数学で学ぶ、直角三角形の合同条件について勉強したいと思います。 // 直角三角形とは? 直角三角形の合同条件 斜辺と1つの鋭角がそれぞれ等しい 斜辺と他の1辺がそれぞれ等しい 直角三角形の証明問題 問題① 〈解答〉 問題② 〈解答〉 問題③ 〈解答〉 直角三角形とは?
三角形の合同条件 三角形の合同条件 合同とは 一方の図形を移動させて他方に重ね合わせることができる場合、この2つの図形は 合同 であるという。 三角形の合同を判断する場合、重ねあわせなくても下記の3つの合同条件のうちどれか一つに当てはまれば合同だといえる。 今回は中2数学で学ぶ、三角形の合同条件について勉強したいと思います。 三角形の合同条件 3つの辺がそれぞれ等しい 2辺とその間の角がそれぞれ等しい 1辺とその両端の角がそれぞれ等しい 三角形の合同条件を使った証明問題 問題① 〈解答〉 問題② 〈解答〉 問題③ 〈解答〉 スポンサー直角三角形の合同条件 直角三角形の合同条件 2つの直角三角形は、次の場合に合同である。 1 斜辺と1つの鋭角が、それぞれ等しいとき(証明) 2 斜辺と他の1辺が、それぞれ等しいとき(証明)
「三角形の合同条件」の3つのうち、 2つに絞る ↓ 2.2つに絞った条件の、どちらかに合うような 辺や角を探す。(ただし仮定以外) この方法で考えると、 合同証明がもっとスムーズに 解けるようになります。 以下で、具体的な問題をお見せしましょう。 三角形の合同条件が3つである理由を考えてみます。 3つの合同条件は3カ所等しいところがあると成立しています。 等しい部分を1カ所のとき、2カ所の時・・・と考えると、これら3つが三角形の合同条件となっている理由が分かりそうです。 等しい部分が1カ所の場合 等しい部分が一カ所合同条件が分かれば、2つの三角形が合同かどうかを数学的に判断することが出来るようになります! そもそも合同って何だっけ? と思う方でも読み進められるように、 合同 について復習できる内容を記事内に入れていますので、良ければ最後まで読み進めていってみてください。
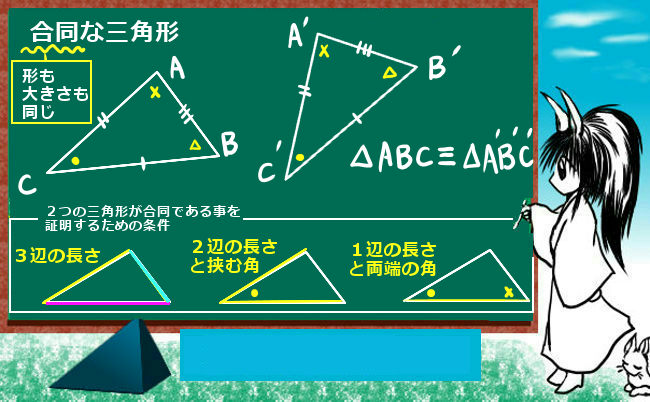



三角形の合同 理数系無料オンライン学習 Kori




三角形の合同条件と それに対応する面積公式 サブロウ丸
三角形の成立条件よりx194 よって これはx>13を満たす。 以上より8以上をまとめれば、『三角形の合同条件』ですね! その前に、少し気づいた点があると思います! (1) 全 辺辺辺角角角のうち、「3つの部分」だけでよい(形、大きさが決まる) ex ①辺・辺・辺 ②辺・辺・角 ③辺・角・角 cf 「3つの部分」が同じということで、 「≡」マークは3本線? はたまた 三角形の合同条件について一つ気づいたことがあったので 適当に調べたらあんまり見つからなかったのと、合同条件丸暗記系の記事が多くてうんざりしたから書く 本当に正しいのかちょっと不安になってる 間違ってたらこっそり教えてね あとあんまりきちっとした数学語を使ったり正
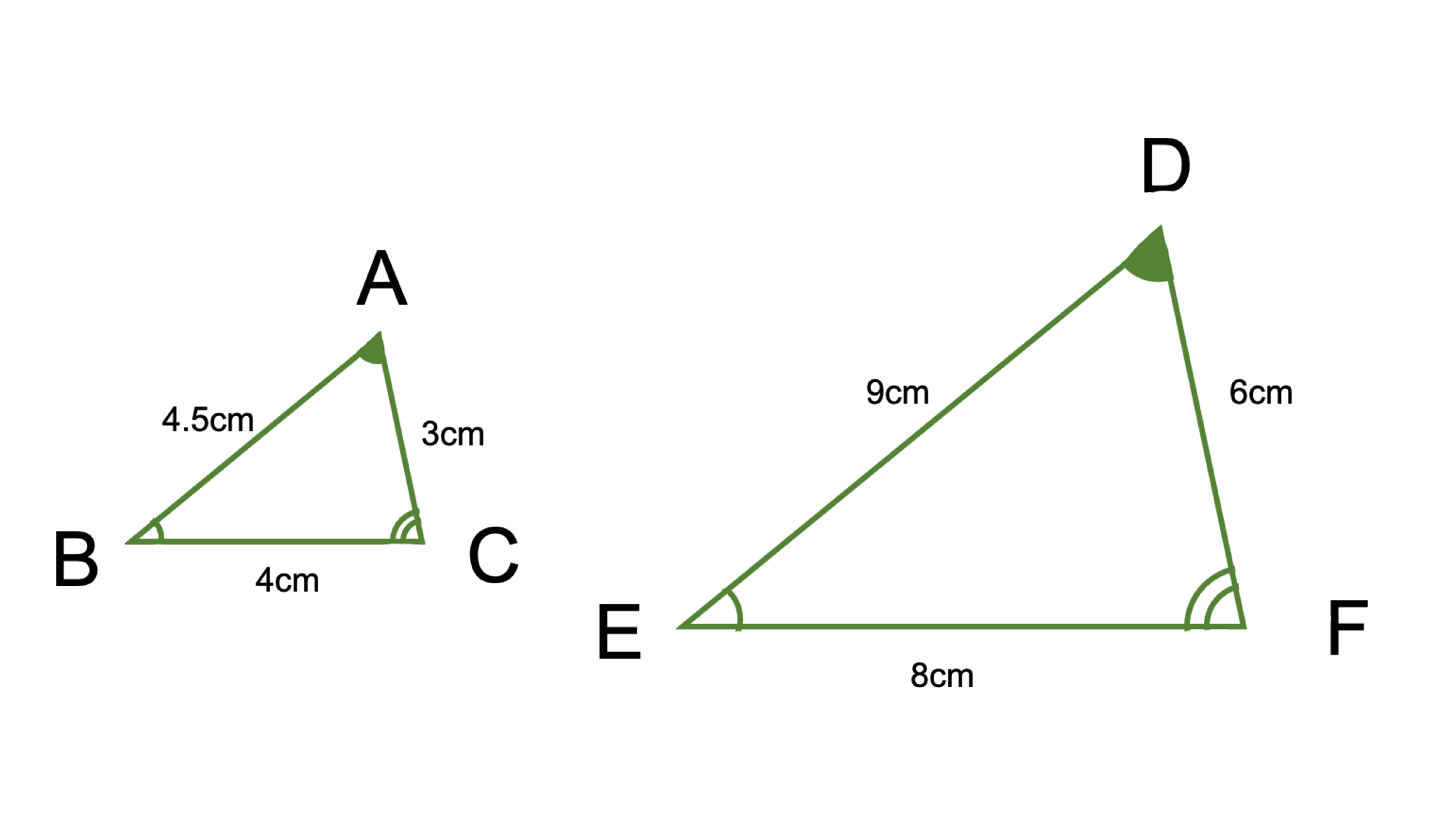



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



直角三角形の合同条件とそれを利用した証明 チーム エン
相似条件と合同条件の違いとは? Tooda Yuuto 18年7月24日 2つの三角形が合同であることを示すための条件を、 三角形の合同条件 と言います。 以下の3つの合同条件のうち、 どれか1つでも成り立っている なら「それらの三角形は合同である」ということが 三角形が完全に決定される場合 1:三辺の長さ a, b, c a,b,c a, b, c が与えられた場合 余弦定理から角 A, B, C A,B,C A, B, C が求まります。 これは,「三辺の長さがそれぞれ等しい三角形は合同である」という事実と対応しています。 合同条件を満たすとなぜ合同なのか?を考えてみる まずは、三角形の合同条件についての復習 まずは、"合同"についての復習です。 "合同"とは、簡単に言えば、2つの図形を比べたとき、形と大きさが同じであることをいいます。 言い換えると、一方の図形を動かしたり裏返したりすると




三角形の合同条件 Youtube




2 の直角三角形の合同条件は何ですか Clearnote
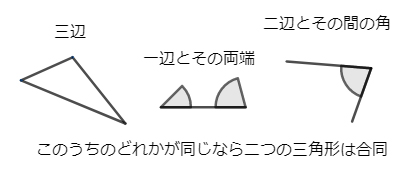
三角形の合同条件とは? 合同な三角形を見つけてみよう! というテーマでお話していきます。 これから 合同の証明問題をやっていく上で 大切となってくる基礎部分なので しっかりと理解しておきましょう! 合同な図形の基本性質については、こちらの記事を参考にしてね! 中学数学3.三角形の合同条件 さて前節では2つの三角形が同じかどうかを確認するのに、6つ全ての特徴を見る必要はないという説明をしました。では 必要最小限の特徴はどこを見ればいいのでしょう?実はこれをまとめたのが、中学校で現れた次の「三角形の合同条件」です。 ① 3つの辺の長さが同じ1 三角形の合同条件(2年) 次の図で,同じ印をつけた辺や角はそれぞれ等しい。あてはまる合同条件を, それぞれ答えなさい。 ⑴ ⑵ ⑶ 次のことがらの仮定と結論を書きなさい。 ⑴ a=b ならば,ac=bc である。 ⑵ xが6の倍数ならば,xは3の倍数である。 ⑶ 長方形の1つの内角は 90ß である
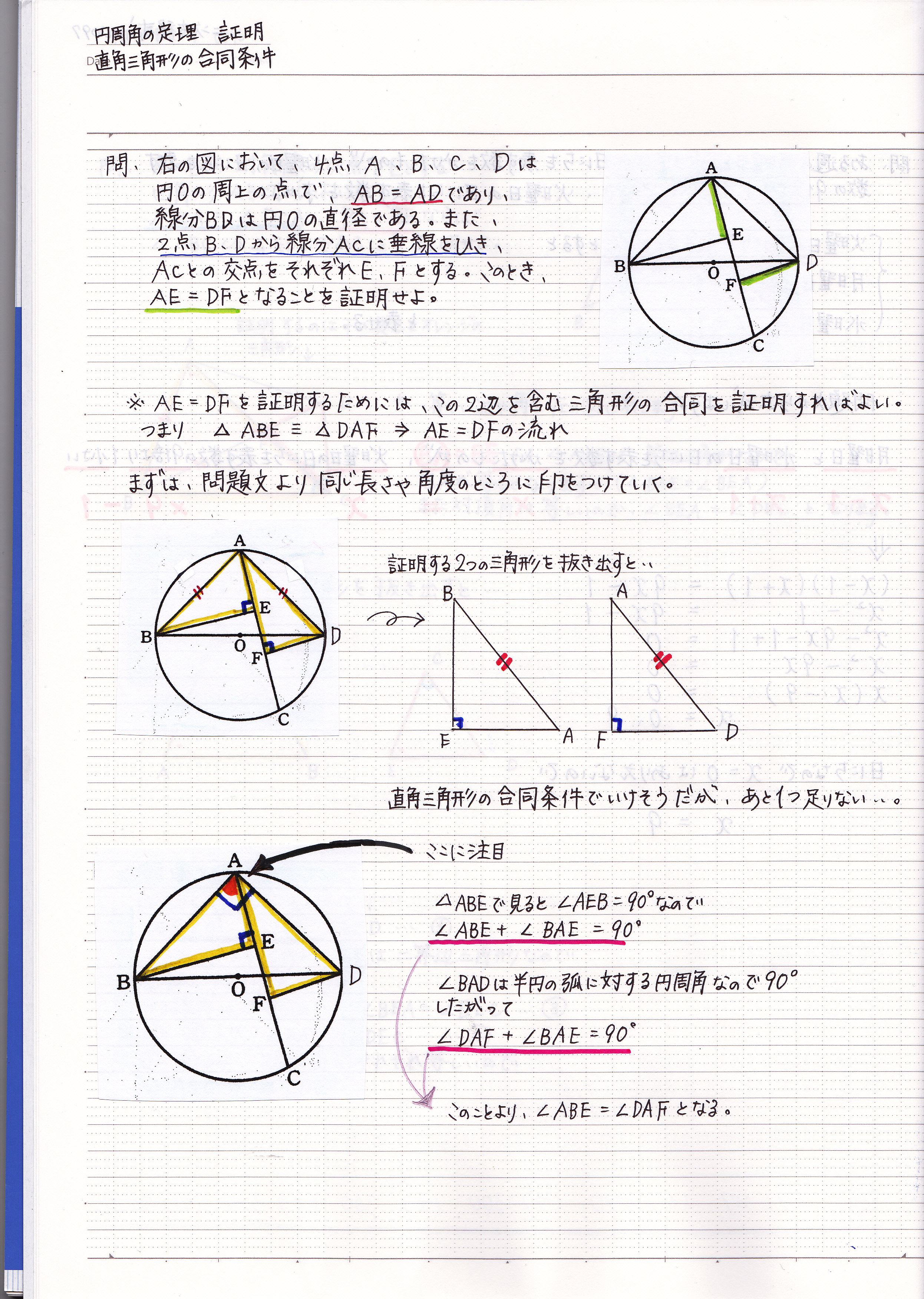



直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方
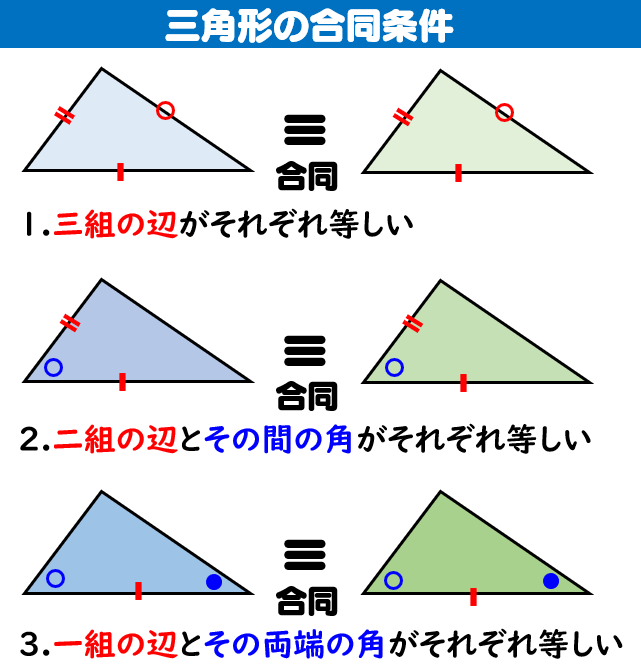



三角形の合同条件と証明問題の解き方 数学fun
仮定と結論,逆,合同条件/三角形の合同の証明/直角三角形/二等辺三角形の定理/ 二等辺三角形の性質を使った証明 /二等辺三角形になることを証明/正三角形/ FdData 入試製品版のご案内 FdData 入試ホームページ掲載のpdf ファイル(サンプル)一覧 ※次のリンクはShiftキーをおしなが




中2数学 三角形の合同条件2 2辺とその間の角 練習編 映像授業のtry It トライイット



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典
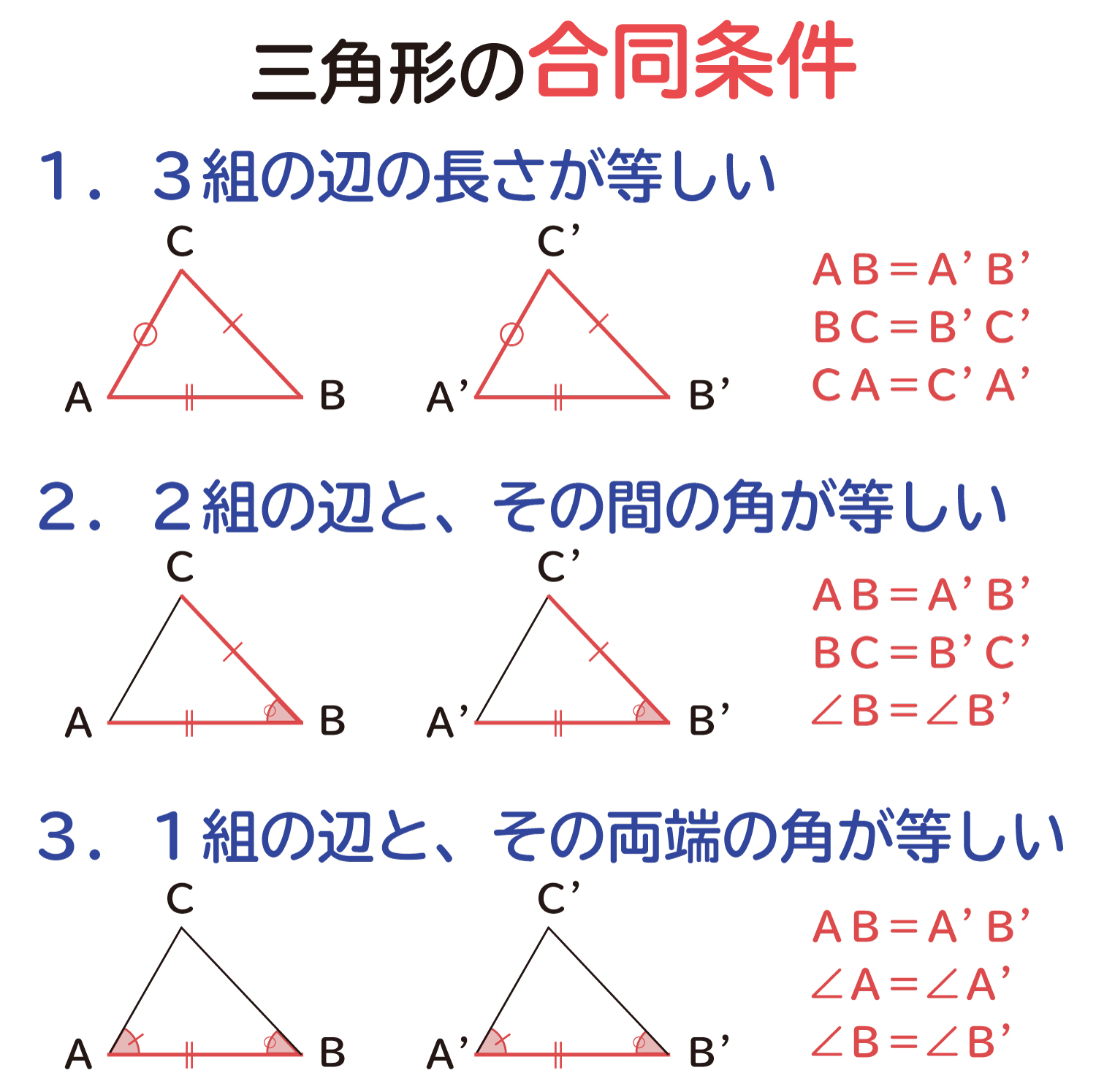



三角形の合同条件の説明 おかわりドリル




中学校数学 証明のコツ 直角三角形の合同条件 と その利用の仕方 を自学自習できる教材




暗記必須 三角形の合同条件を見やすい図で一発理解しよう 高校生向け受験応援メディア 受験のミカタ




直角三角形の合同条件を使った証明とは なぜ2つ増えるのか 遊ぶ数学
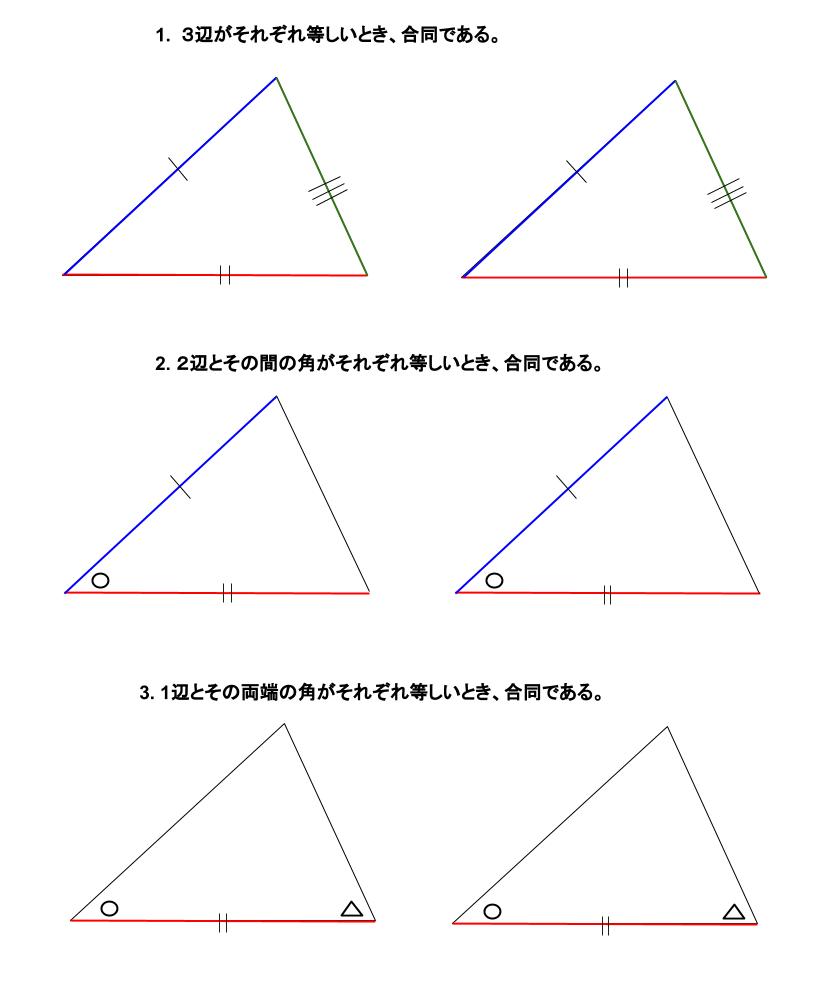



中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su
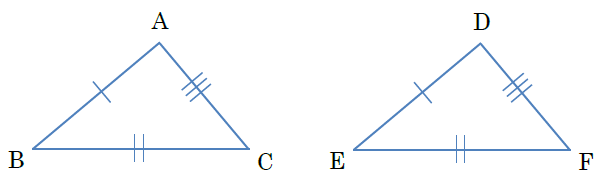



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




直角三角形の合同条件再び 中学校2年生の数学 身勝手な主張




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン
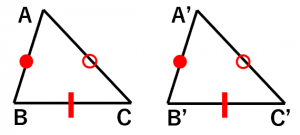



三角形の合同条件を図で分かりやすく説明 具体例で学ぶ数学




中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾
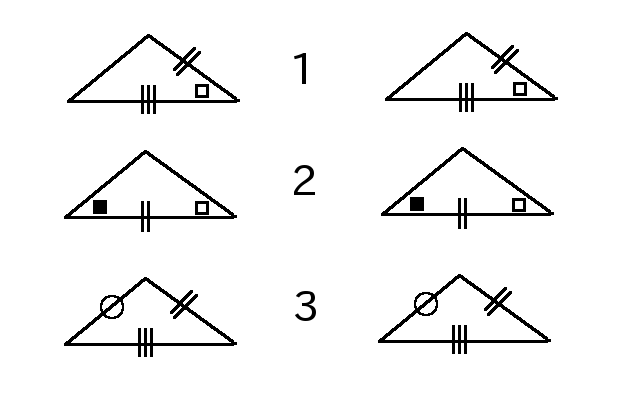



File 三角形の合同条件 Png Wikimedia Commons



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典
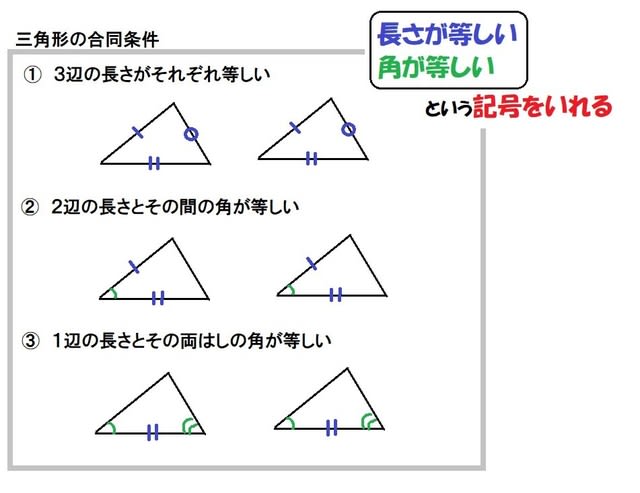



上数学合同条件 ニスヌーピー壁紙




直角三角形邊長比三角形的邊長比 Wfklee



中学数学証明問題です 直角三角形の合同条件はわかるのですが Yahoo 知恵袋
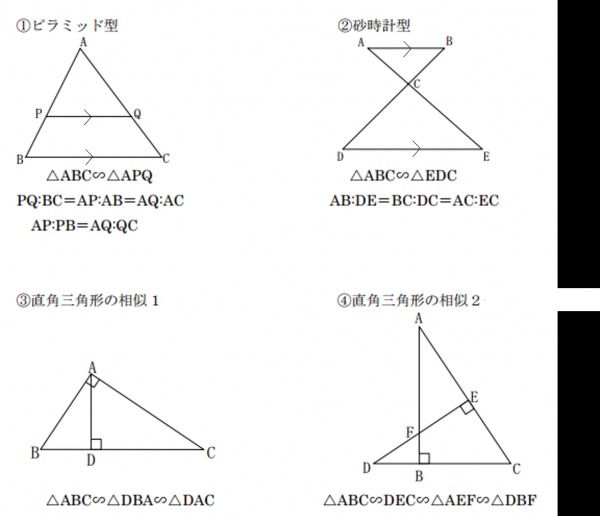



三角形の相似 合同条件 優技録
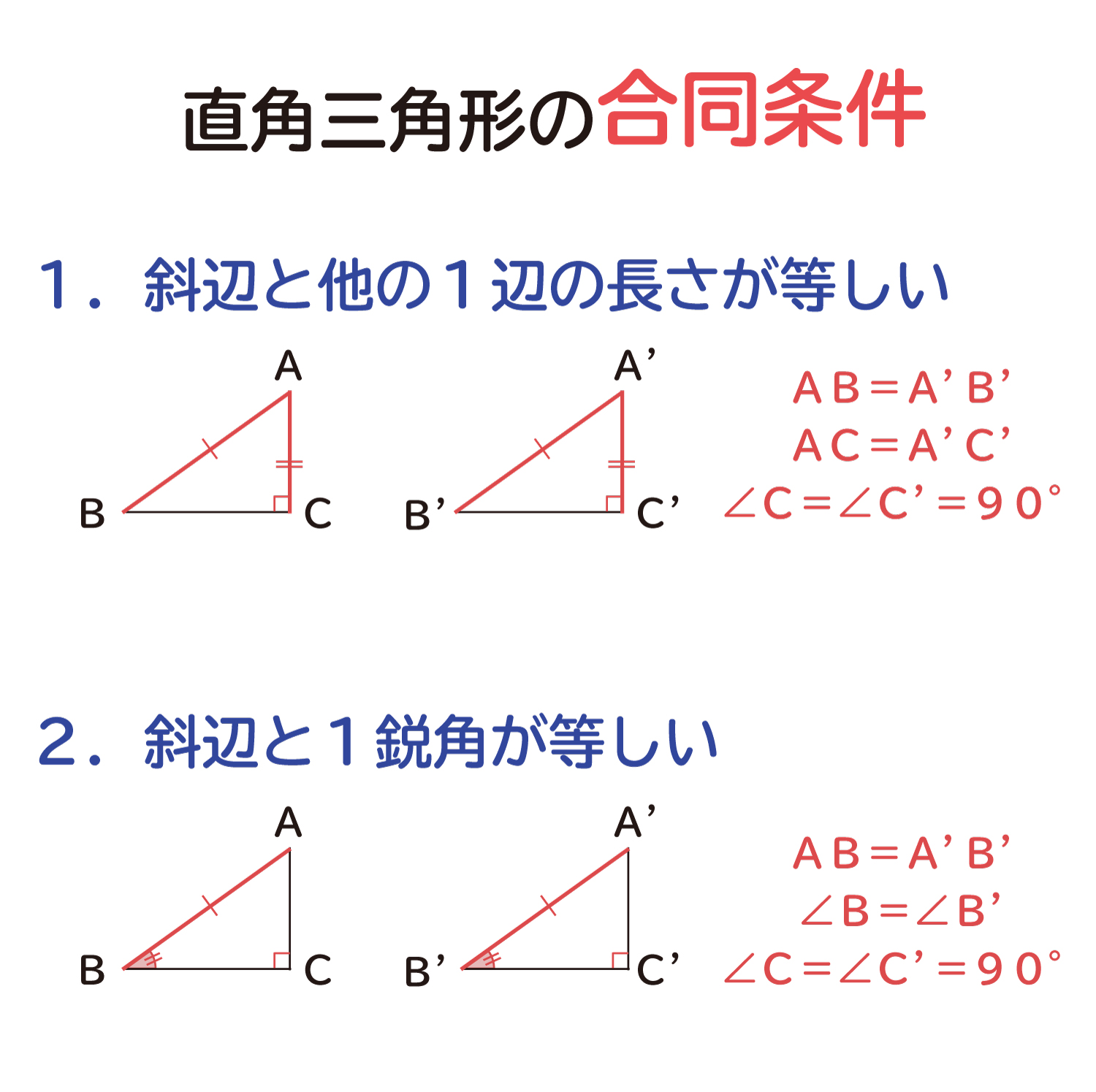



直角三角形の合同条件の説明 おかわりドリル



本時のねらい 直角三角形の合同条件を導き それを理解し 証明ができるようにする Ppt Download
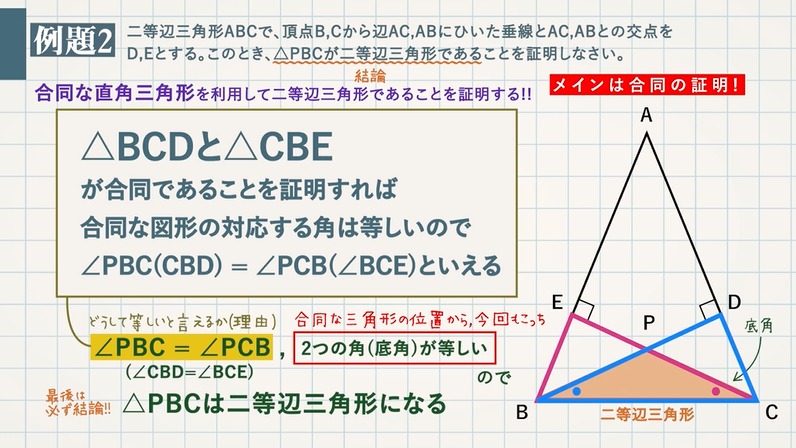



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
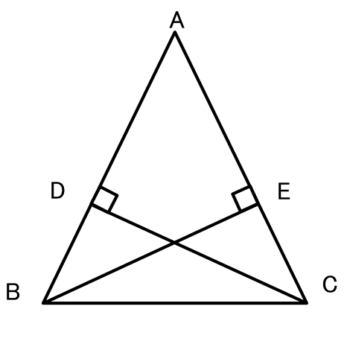



フロー 2 5 4 4 直角三角形の合同条件を利用した証明
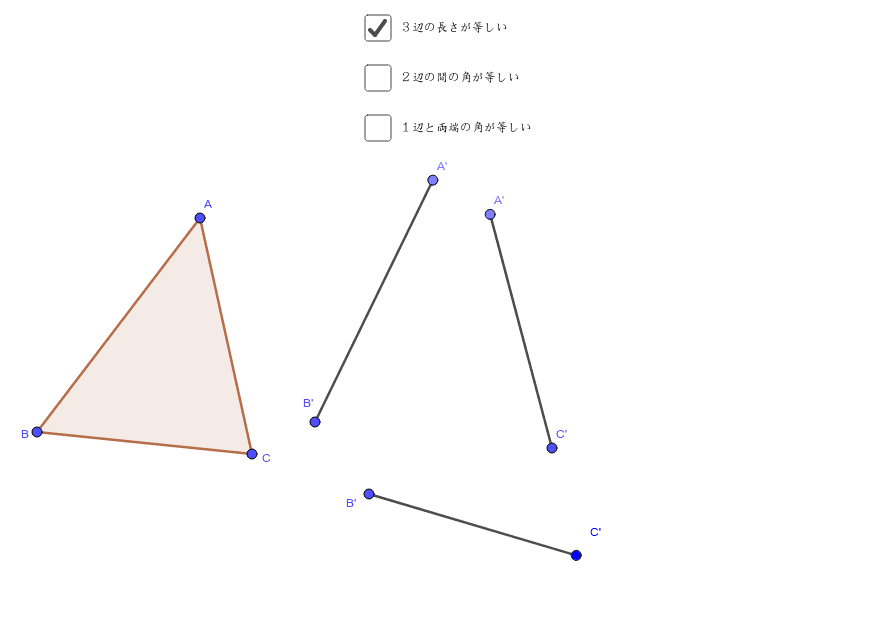



三角形の合同条件 Geogebra




5分でわかる 三角形の3つの合同条件 Qikeru 学びを楽しくわかりやすく




演習 直角三角形の合同条件 Youtube



三角形 合同 相似条件 直角三角形の合同条件 中学 数学 理科の復習サイト




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学




三角形の合同条件 中学数学 By じょばんに マナペディア



数学のアレ 何に役立つ 三角形の合同条件 同じ形の三角形を見つけて テストで5点くらいもらう 以外の使い方 1 2 ページ ねとらぼ




中2数学 チョー便利な直角三角形の2つの合同条件 Qikeru 学びを楽しくわかりやすく



中学数学 直角三角形の合同条件 中学数学の無料オンライン学習サイトchu Su




三角形の合同条件




直角三角形の合同 条件 について 苦手な数学を簡単に



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ
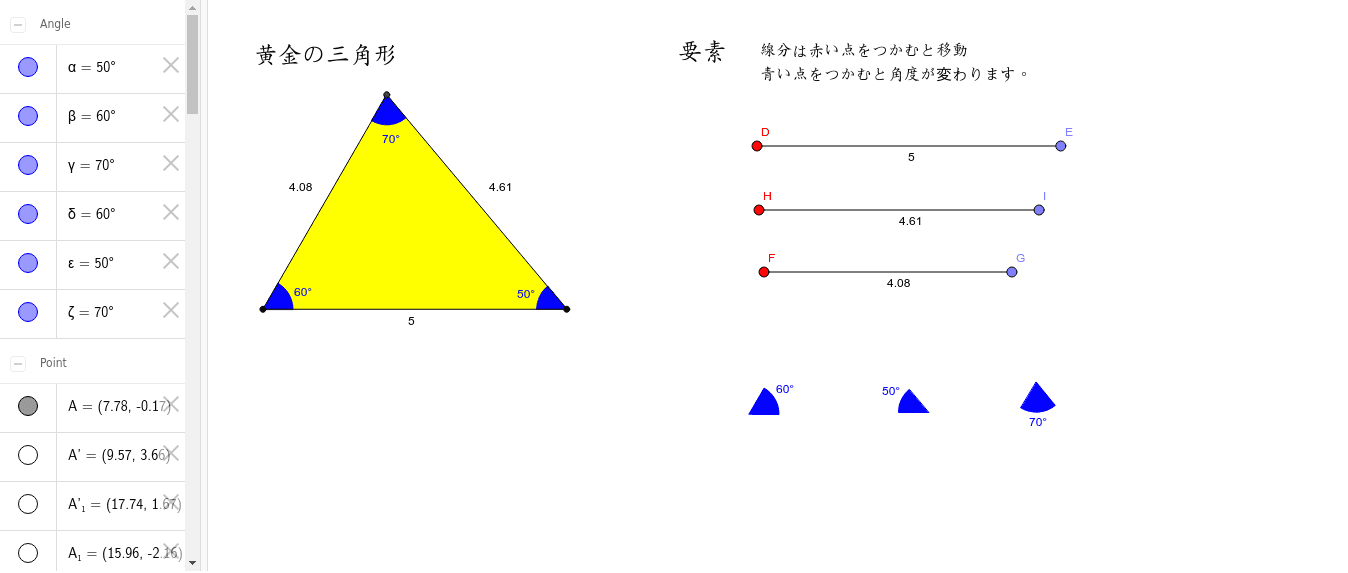



三角形の合同条件を見つける Geogebra




暗記必須 三角形の合同条件を見やすい図で一発理解しよう 高校生向け受験応援メディア 受験のミカタ
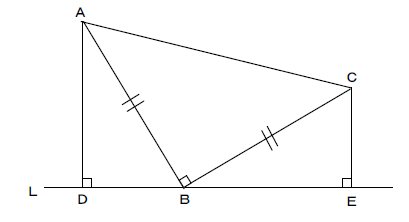



中2数学 直角三角形の合同条件を使った証明の定期テスト過去問分析問題 ダイスト
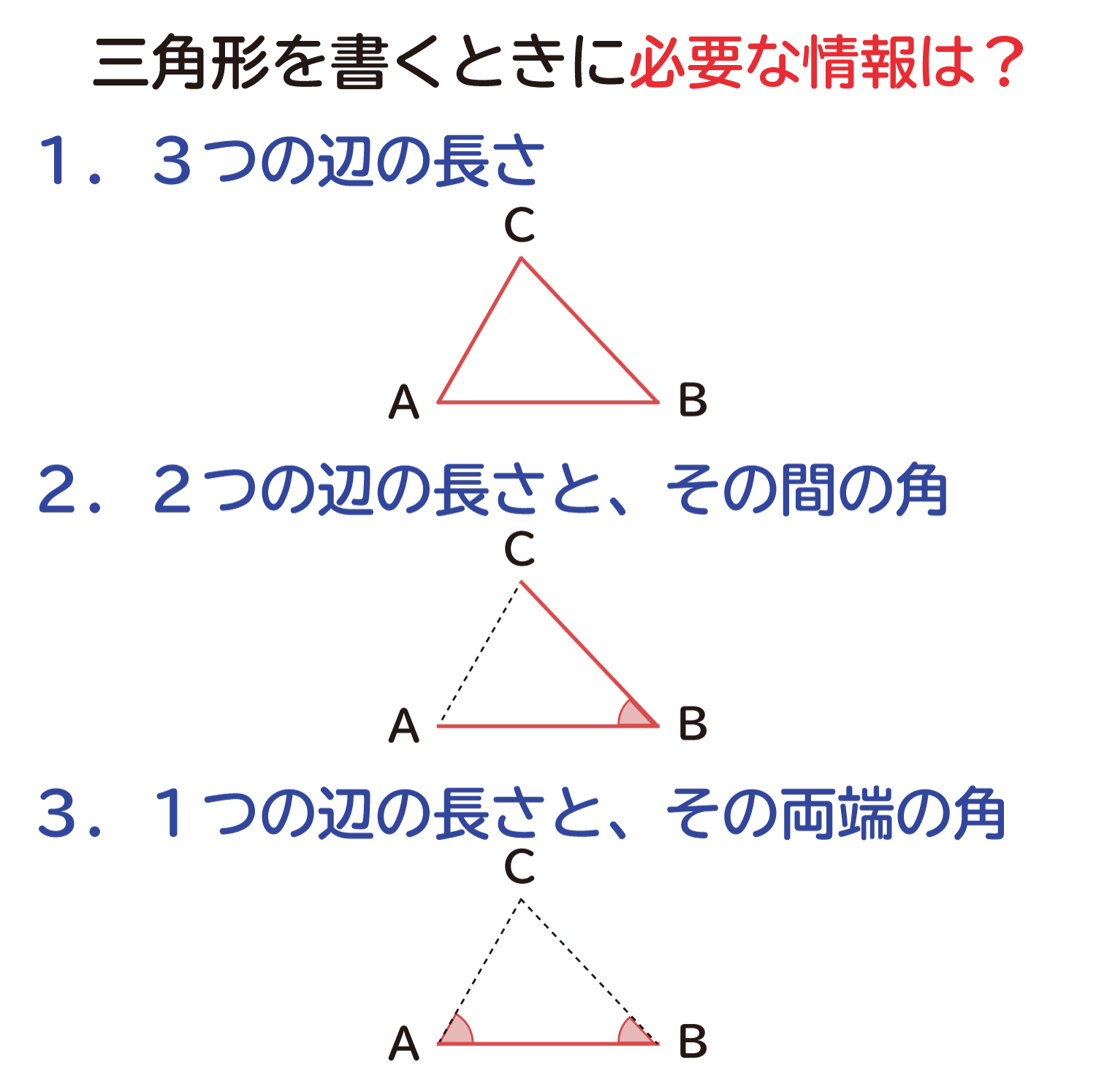



三角形の合同条件の説明 おかわりドリル
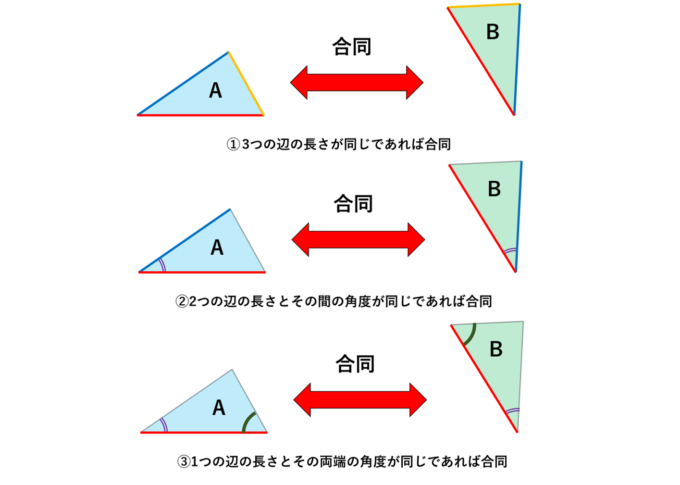



合同条件について本気出して考えてみた 前編 数学 統計教室の和から株式会社



3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ




三角形の合同条件で 3組の角はそれぞれ等しい Clearnote




三角形の合同条件 イ弋マ本ゼミナール




三角形の合同条件を使った証明問題 中学2年生の問題を解こう 身勝手な主張
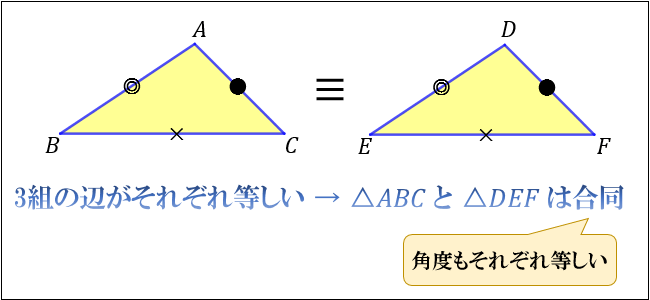



三角形の合同条件 相似条件と合同条件の違いとは アタリマエ
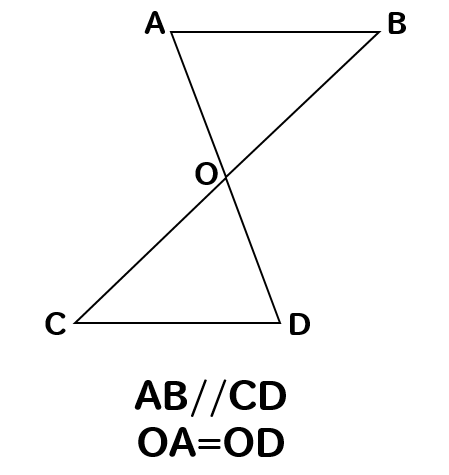



三角形の合同条件 合同な図形の見つけ方 証明問題の基礎を身につけよう 数スタ
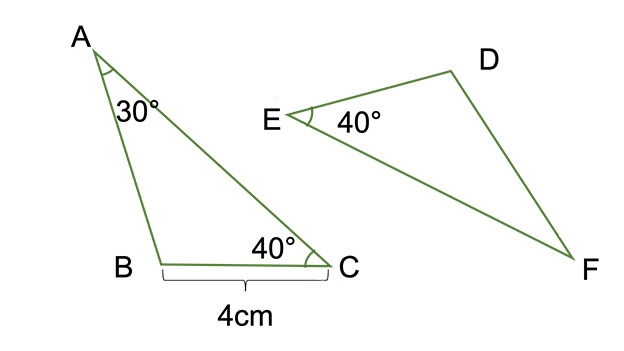



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




直角三角形の合同条件 証明のときに直角三角形が出てきたらこれ 中学や高校の数学の計算問題
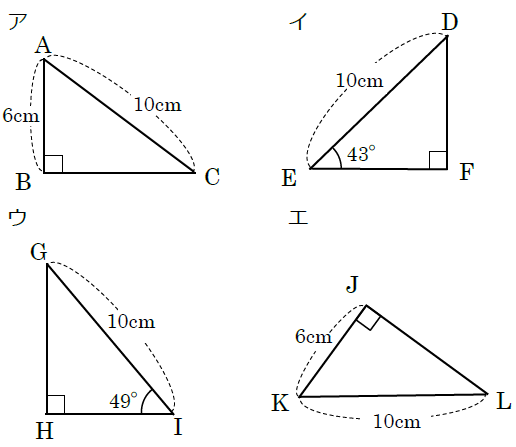



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン
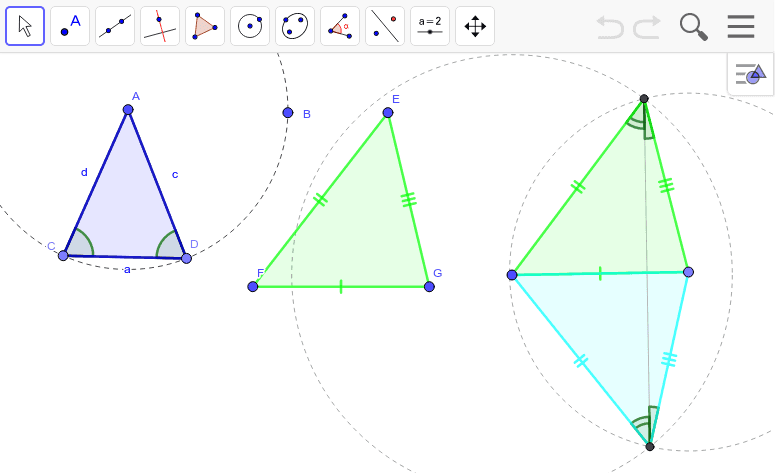



三角形の合同条件3辺 Geogebra




高校英語を指導できる人を探そうか悩んでるシグマゼミ そういや 中2の 三角形の合同条件 とかさ 中学でよくある 一字一句この通りに書かないと減点 なものの代表格だと思うんだけど あれ 教科書によってびみょーにちがったりしないの 写真は 学校




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学
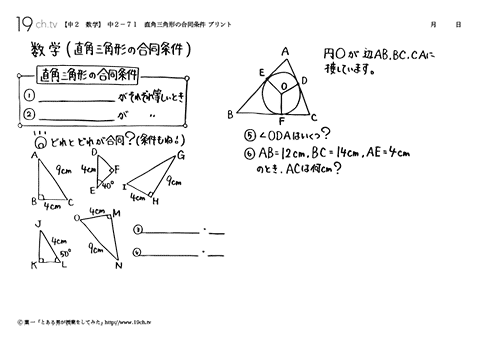



中学2年の数学 動画 直角三角形の合同条件の問題 19ch
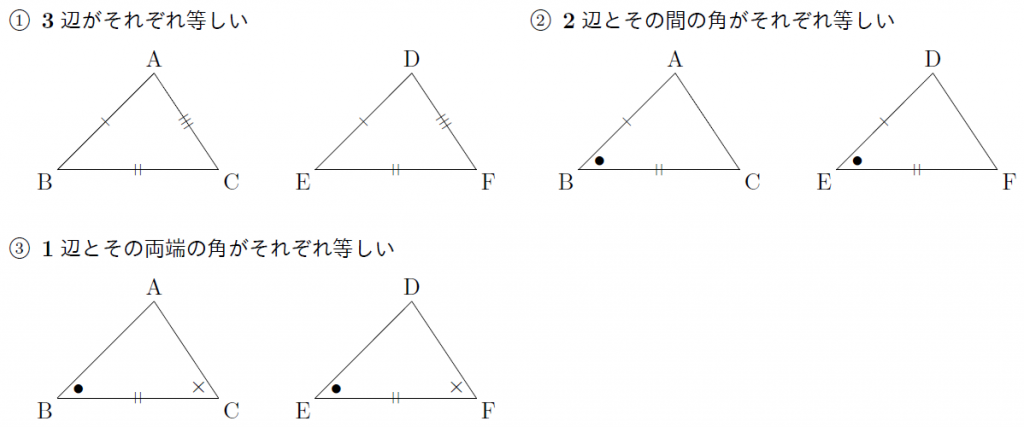



三角形の合同条件 まなびの学園




第4の三角形の合同条件 豆もあいの決して心の折れることのないブログ
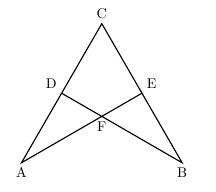



三角形の合同の問題の解法 夢を叶える塾
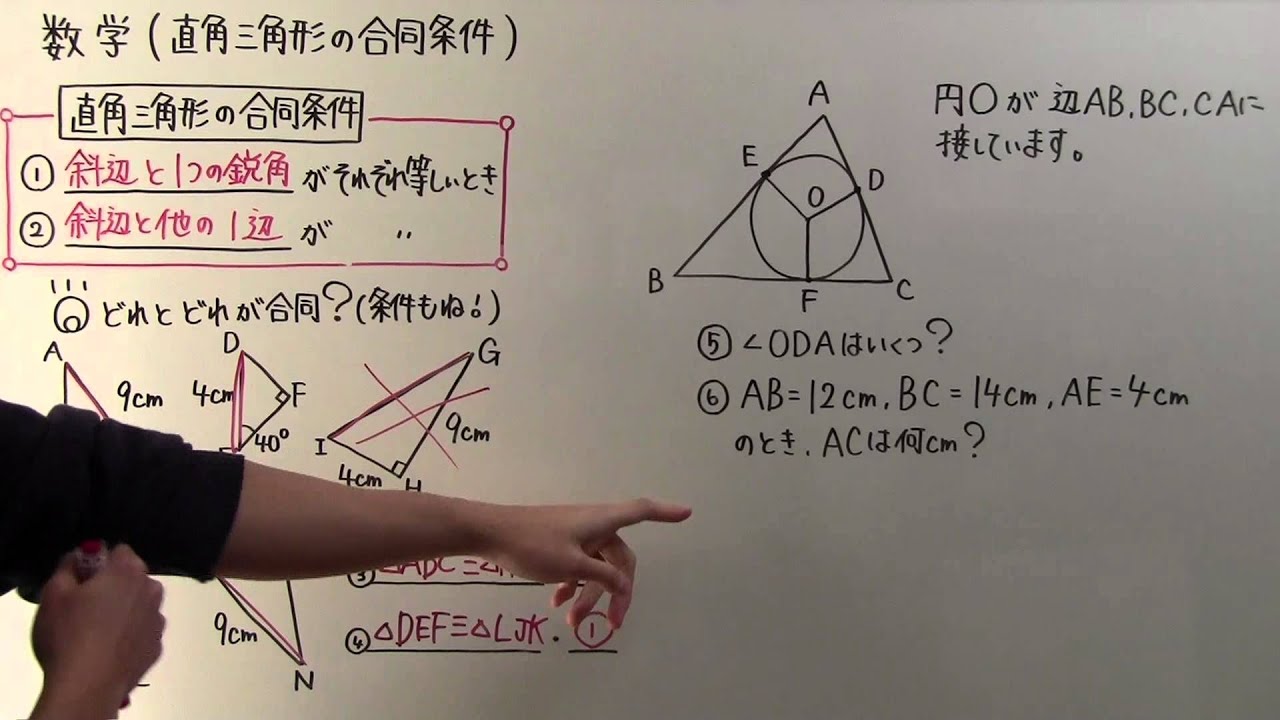



数学 中2 71 直角三角形の合同条件 Youtube
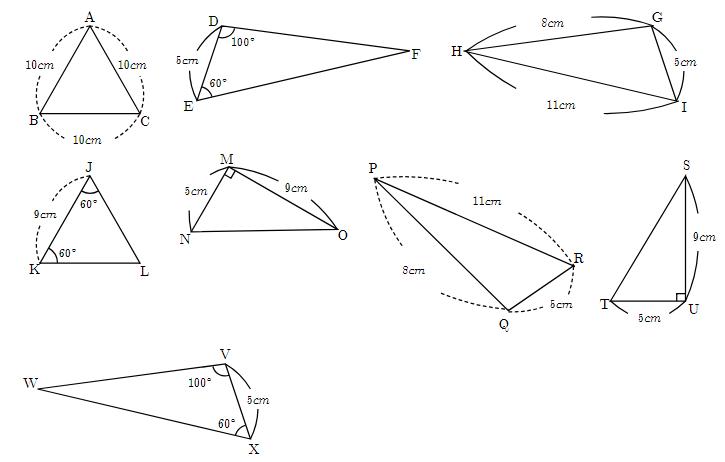



中2数学 三角形の証明の仕方 Pikuu




三角形の合同条件についての質問です 三角形の合同条件で 2つの辺と 数学 教えて Goo
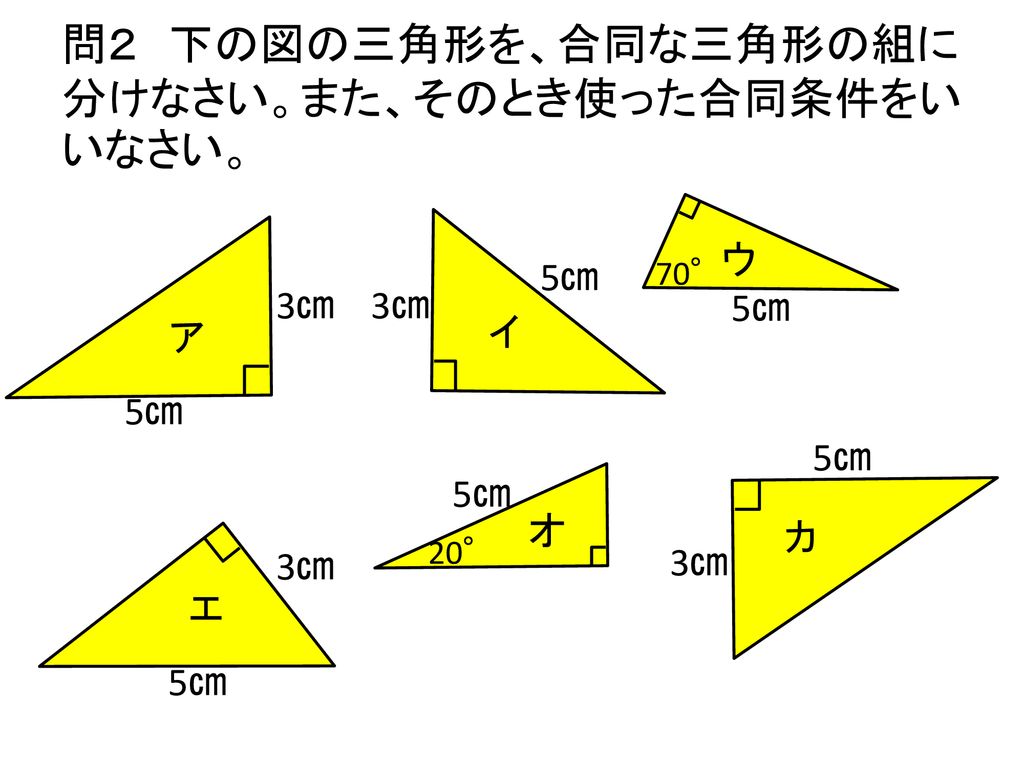



本時のねらい 直角三角形の合同条件を導き それを理解し 証明ができるようにする Ppt Download



2




合同と証明 Ict教材eboard イーボード



合同な図形とは 三角形の合同条件 教遊者




合同条件について Blogskol
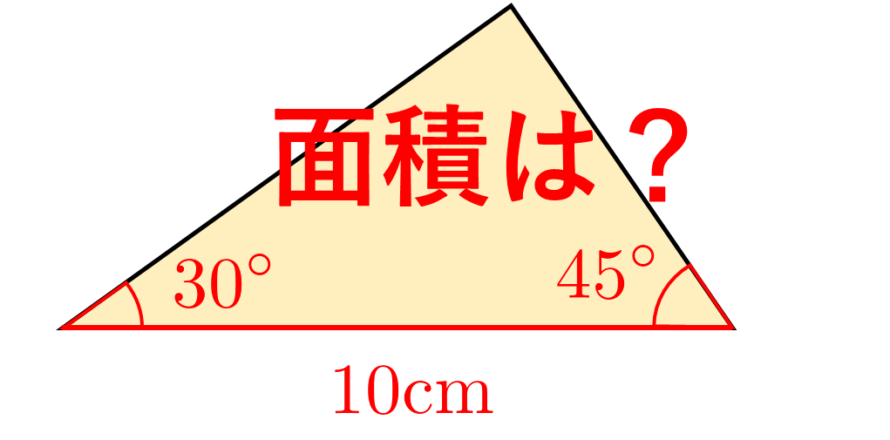



三角形の合同条件と面積 数学 統計教室の和から株式会社
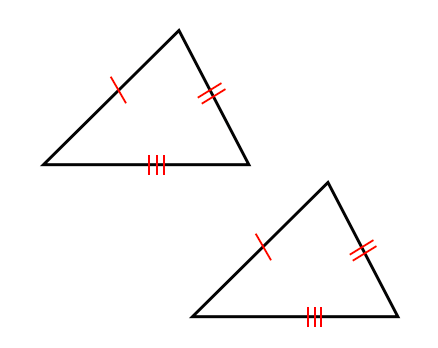



三角形の合同条件を知ろう 苦手な数学を簡単に




中2数学 三角形の合同条件3 1辺とその両端角 映像授業のtry It トライイット




工程建设项目合同管理通识第二弹来了 每日头条




中2 三角形の合同条件 注意したい点 ポイントまとめ 中学生 数学のノート Clearnote
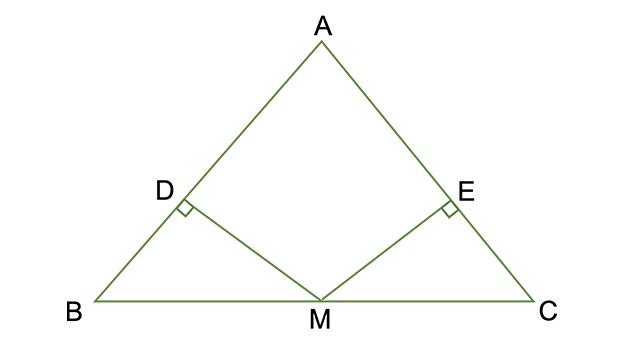



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
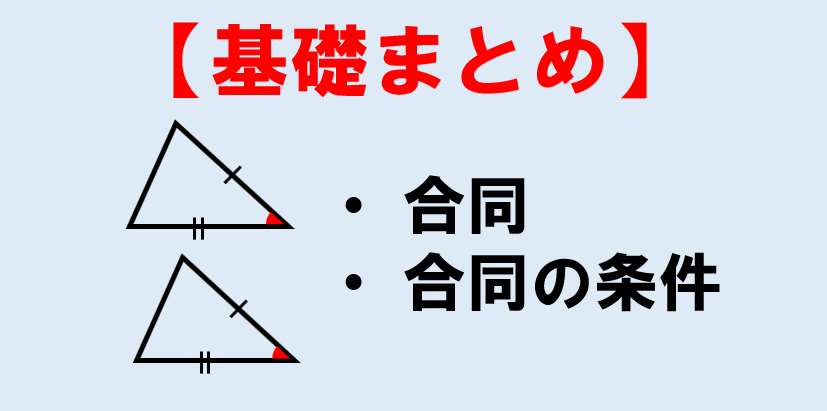



中2数学 合同 三角形の合同条件まとめ 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




三角形の合同条件
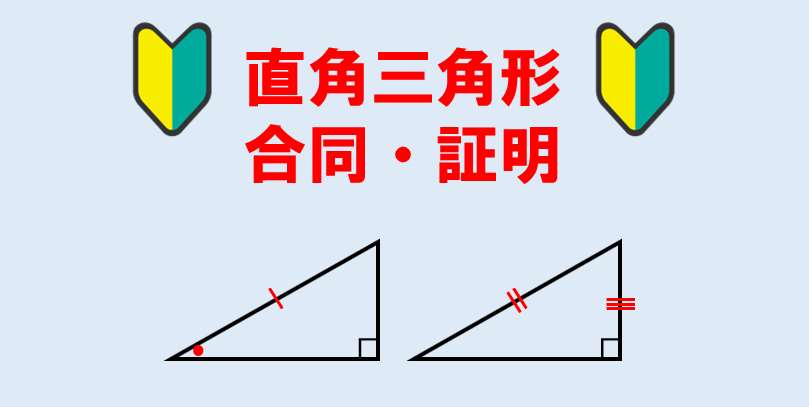



中2数学 直角三角形の合同条件と証明問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
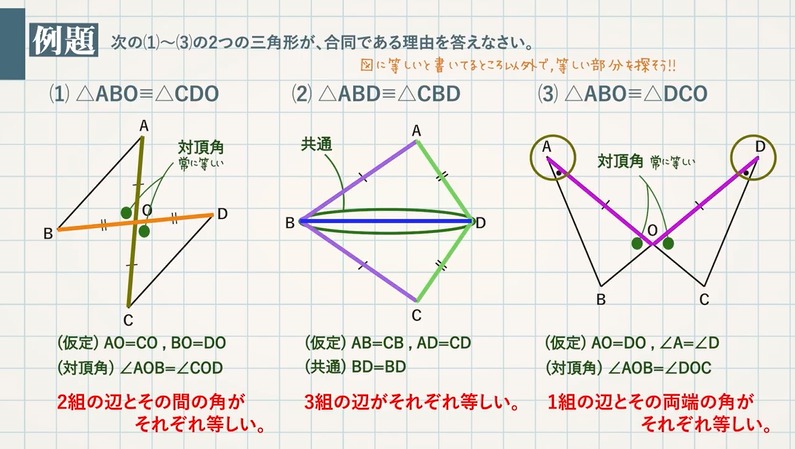



合同な図形とは 三角形の合同条件 教遊者
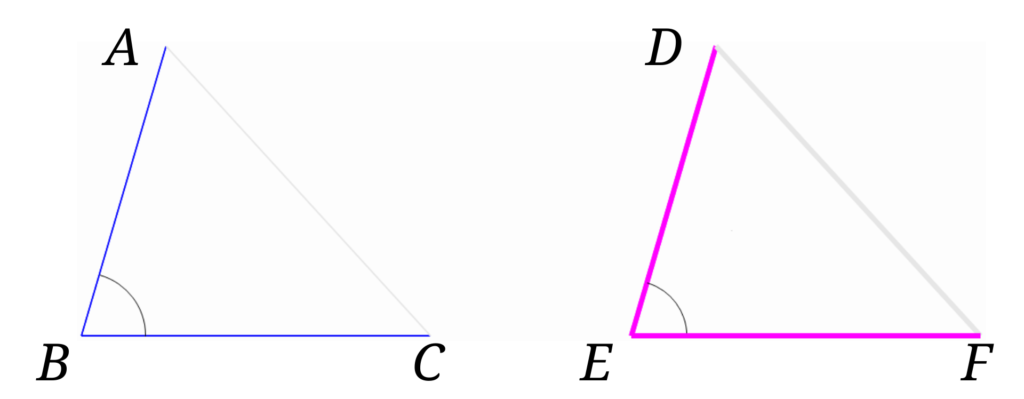



三角形の合同条件の表現ってなぜこの3つなの まぜこぜ情報局
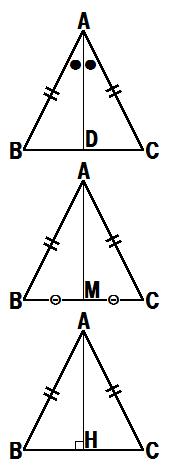



三角形の合同条件と二等辺三角形の底角 2 算数 数学記事



三角形の合同条件 まいにち一題 中学受験過去問題研究
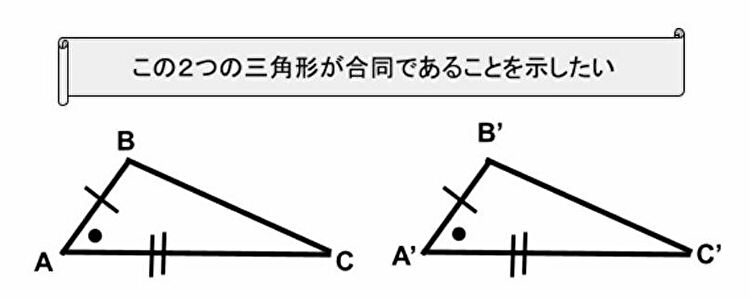



公理から手繰る 三角形の合同条件の証明 二辺挟角 Sas 数学探求 ぱるきちどっとこむ




直角三角形の合同条件とその証明 数学fun




工程建设招标设标合同条件 第1部分 Word模板下载 熊猫办公




三角形の合同条件




三角形の合同条件 小学算数 算数 小5 数学中2 三角形 Youtube



三角形の 合同条件 相似条件 の意味について 三角比や正弦定理 余弦定理の理解も深くなる ここからはじめる高校数学



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




三角形の合同条件 小学生 中学生の勉強




直角 三角形 合同 条件 中学校数学自宅学習2年 直角三角形の合同条件



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




三角形の合同条件 合同の証明問題と解き方のコツ リョースケ大学
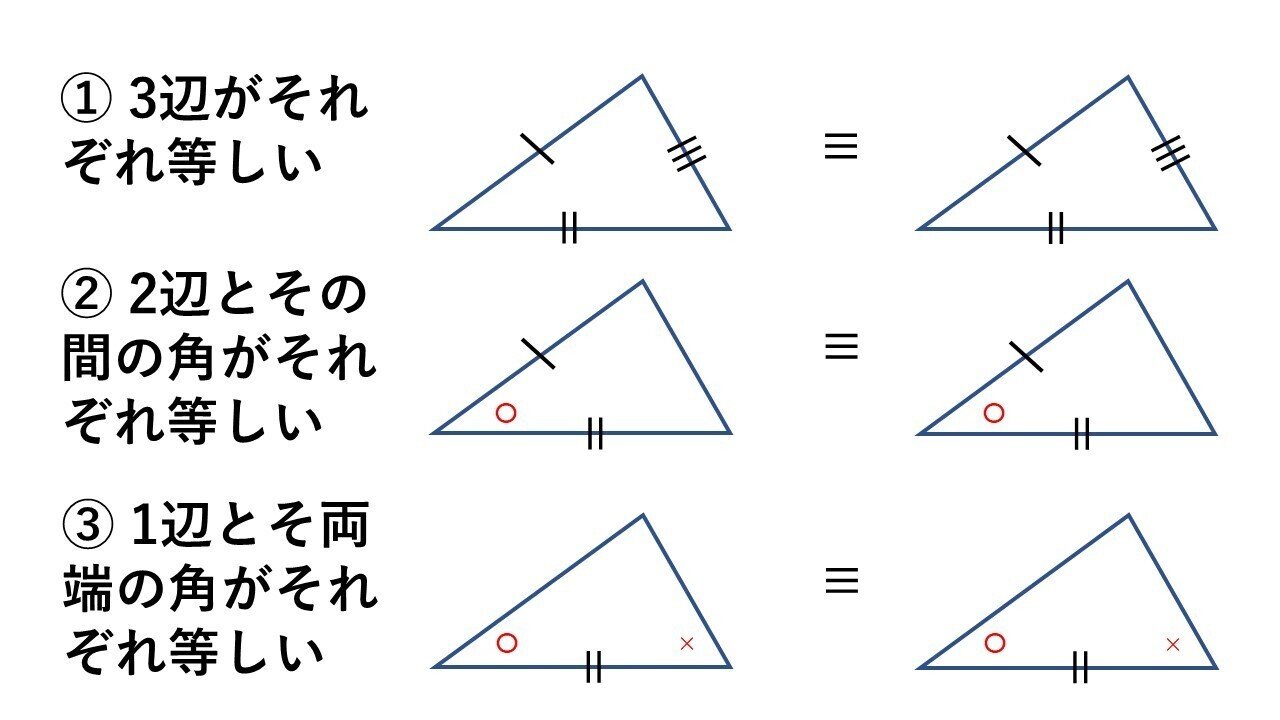



三角形の合同条件から証明へ タロウ岩井の数学 Note
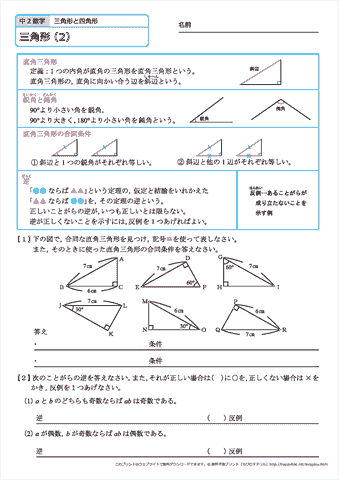



中学2年生 数学 三角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
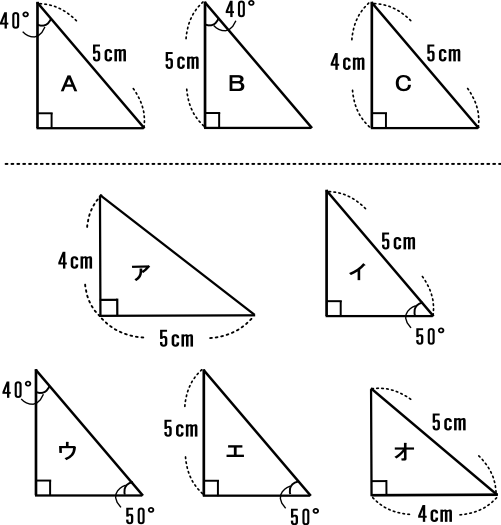



中学2年数学練習問題 直角三角形の合同条件と証明問題 図形と合同
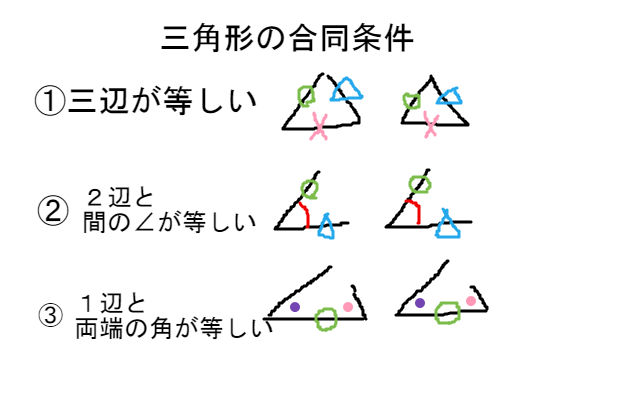



三角形の相似 合同条件 中学 数学 理科の復習サイト



中学数学 図形の合同 図形の性質
コメント
コメントを投稿